

You can figure out and contribute to our open source project on our git hub repo.Consider the response of a linear System to an arbitrary input x. Open-source project: Open source is very very important for us that's why we are contributing to open-source development as well. Real-time chat: We have an extensive amount of geeks behind the scene they are helping you to solve every problem you are facing real-time Voice APIs:- Every question and answers have voice APIs by pressing the listen to this question button user will be able to listen to the content which helps students from different background.Īlgorithm driven video delivery: Every video from our database is delivered against the content which students are browsing with the help of our proprietary algorithm.Įduladder career: We have a robust ATS developed on the top of famous open source ATS called open cats the APIs which we have built on the top of the same will deliver the best and suitable job to the visitor who is browsing in our platform. Question and answers:- Where every question is asked and answered by community and the best question and answers are voted up so the visitors will get the best answers. If area S, in the x-y plane, is bounded by a triangle with vertices (0, 0), (10, 1) and (1, 1), the value of 2 S xy y dxdy ï€ ïƒ²ïƒ² is _. Then the overall impulse response of the cascaded system is given by GATE-Instrumentational Engineering-2013Ī linear time invariant (LTI) system with the transfer function Two systems with impulse responses h1 (t) and h2 (t) are connected in cascade. The time taken by the system output c(t) to reach 94% of its steady-state value lim t→∞ c(t), rounded off to two decimal places, is:
#A BIBO STABILITY CONDITION FOR A CONTINUOUS TIME LTI SYSTEM ISO#
If the A- matrix of the state space model of a S ISO linear time invariant system is rank deficient, the transfer function of the system must have GATE-Instrumentational Engineering-2013Ĭonsider a causal second-order system with the transfer function G(s) = 1/ (1 + 2s + s 2) with a unit-step R(s) = 1/ s as an input. Which one of the following statements about the system is TRUE? Which one of the following options correctly describes the locations of the roots of the equationĪ discrete-time all-pass system has two of its poles at 0.25ïƒ∀ and 2ïƒ∃0. Which one of the following impulse responses is NOT the output of a causal linear time-invariant system?
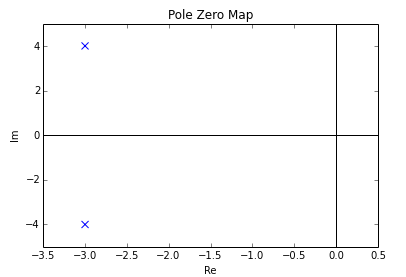
The symbols, a and T, represent positive quantities, and u(t) is the unit step function. Frequency-domain condition for linear time invariant systems. The zero at the origin has multiplicity 4. The proof for continuous-time follows the same arguments. The pole-zero diagram of a causal and stable discrete-time system is shown in the figure. Which of the following statements is NOT TRUE for a continuous time causal and stable LTI system? GATE-Instrumentational-Engineering-2013Ī system is defined by its impulse response h(n) =2^nu(n-2). The input x(t) and the output y (t) of a continuous-time system are related asĪ closed-loop control system is stable if the Nyquist plot of the corresponding open-loop transfer function. The system is BIBO stable if (A) 0 3 (C) 0 6Ĭonsider a single input single output discrete-time system with x as input and y as output, where the two are related as

The characteristic equation of a linear time-invariant (LTI) system is given by ∆(s) = s^4 + 3s/3 + 3s/2 + s + k = 0. The condition on α for which the system is Bounded-Input Bounded-Output (BIBO) stable is

The input x and output y of a discrete-time system are related as y = αy + x. Which one among the following is correct?Ĭonsider the following statements for continuous-time linear time invariant (LTI) systems There is non causal and BIBO stable system with a pole in the right half of the complex plane. There is no bounded input bounded output (BIBO) stable system with a pole in the right half of the complex plane. Consider the following statements for continuous-time linear time invariant (LTI) systems.


 0 kommentar(er)
0 kommentar(er)
